( اذا قطع قاطع مستقيمين في مستوى وكان عموديا على كل منهما فإن المستقيمين )
اذا قطع قاطع مستقيمين في مستوى وكان عموديا على كل منهما فإن المستقيمين متوازيين
مقدمة

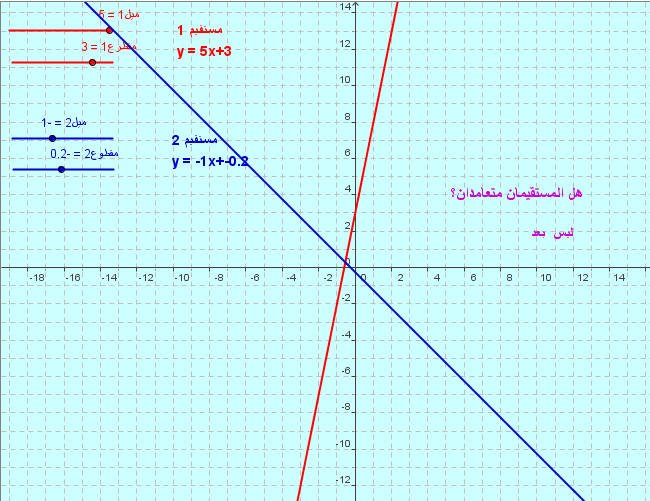
في الهندسة الإقليدية، عندما يتقاطع مستقيم مع مستقيمين آخرين في نفس المستوى ويكون عموديًا على كليهما، فإن المستقيمين متوازيين. هذا هو أحد أهم النظريات في الهندسة والذي يستخدم على نطاق واسع في حل العديد من المسائل الهندسية.
المستقيمات العمودية والمتوازية
تعريف المستقيم العمودي

المستقيم العمودي هو مستقيم يتقاطع مع مستقيم آخر بزاوية قائمة (90 درجة).
تعريف المستقيمات المتوازية
المستقيمات المتوازية هي مستقيمات تقع في نفس المستوى ولا تلتقي أبدًا مهما امتدت.
نظرية القاطع العمودي
إذا قطع قاطع مستقيمين في مستوى وكان عموديًا على كل منهما، فإن المستقيمين متوازيين.
إثبات النظرية
لنفترض أن لدينا مستقيمين AB و CD في مستوى، ومستقيم EF يقطعهما ويتقاطع مع AB عند النقطة X ومع CD عند النقطة Y.
لنفترض أيضًا أن EF عمودي على AB عند X وعمودي على CD عند Y.

نريد أن نثبت أن AB متوازٍ مع CD.
بما أن EF عمودي على AB عند X، فإن زاوية XEF قائمة (90 درجة).
وبالمثل، بما أن EF عمودي على CD عند Y، فإن زاوية YEF قائمة (90 درجة).
وبالتالي، فإن زاوية XEF وزاوية YEF متساويتان، وكلاهما يساوي 90 درجة.
هذا يعني أن المستقيمين AB و CD متوازيين، لأن زوايا متقابلة متساوية.
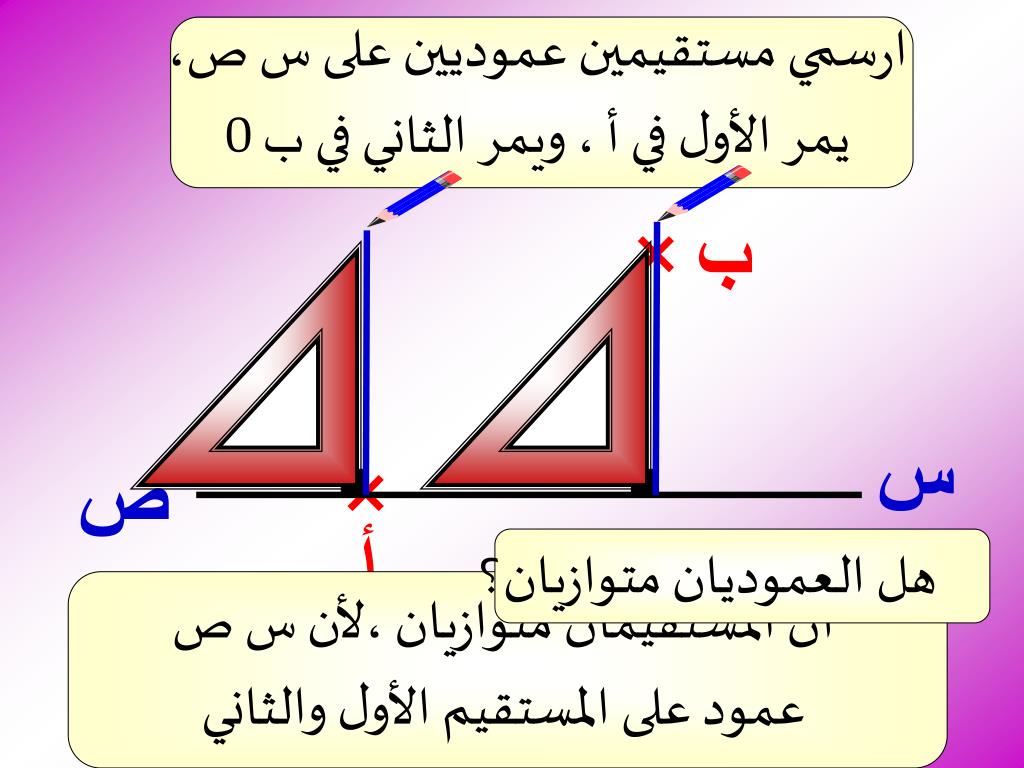
تطبيقات نظرية القاطع العمودي

تُستخدم نظرية القاطع العمودي في مجموعة واسعة من التطبيقات في الهندسة، بما في ذلك:
إيجاد المسافات بين المستقيمات المتوازية

رسم خطوط متوازية
إثبات أن المستقيمات متوازية
حل معادلات هندسية
استنتاج
نظرية القاطع العمودي هي نظرية أساسية في الهندسة والتي تستخدم على نطاق واسع في مجموعة متنوعة من التطبيقات. تساعد هذه النظرية في فهم العلاقة بين المستقيمات العمودية والمتوازية وتوفر أداة قوية لحل المسائل الهندسية.