( ميل المستقيم في الشكل المجاور هو )
ميل المستقيم في الشكل المجاور

يمثل الميل رقمًا يصف مدى انحدار الخط المستقيم. يُحسب عن طريق قسمة التغير في الارتفاع (Δy) على التغير في المدى (Δx) بين نقطتين على الخط.
في الشكل المجاور، يتم إعطاء ميل المستقيم بالصيغة:
الميل = Δy / Δx
حيث Δy = (y2 – y1) و Δx = (x2 – x1)
1. تحديد النقطتين
لتحديد ميل المستقيم، نحتاج إلى تحديد نقطتين عليه. دعونا ندعو هاتين النقطتين (x1، y1) و (x2، y2).
في الشكل المجاور، نختار نقطتين: (2, 1) و (4, 3).

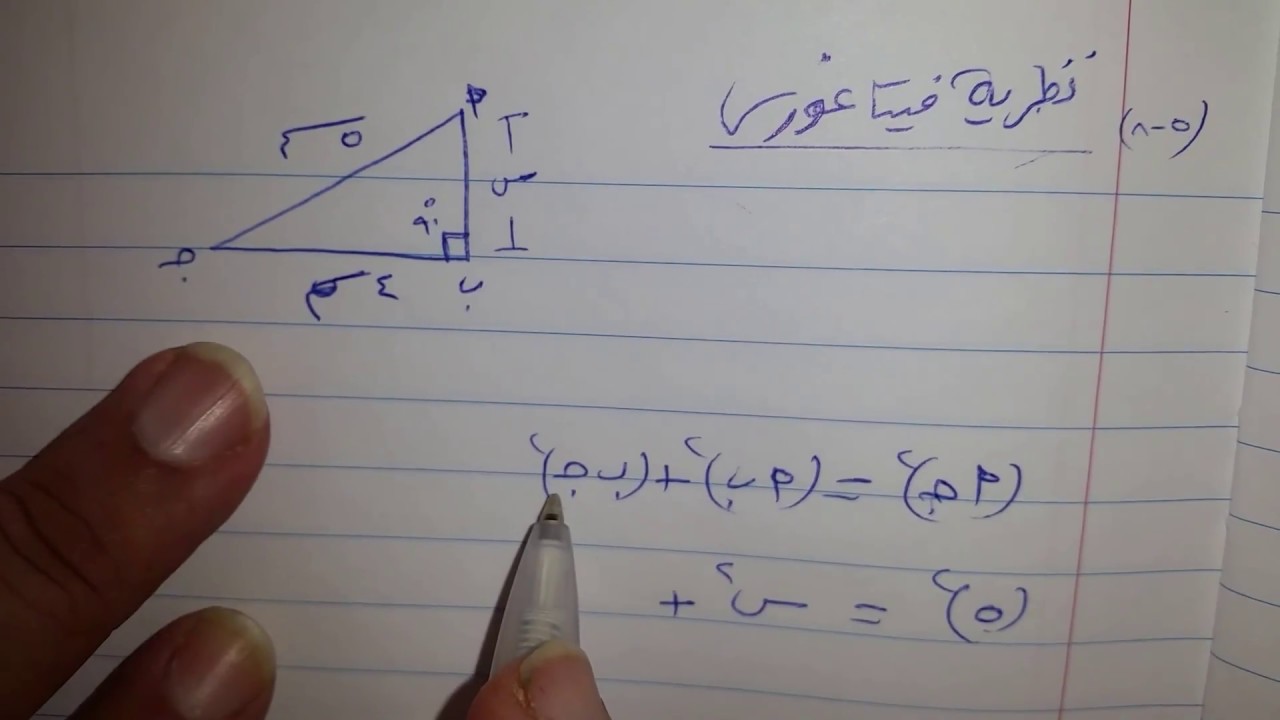
باستبدال هاتين النقطتين في الصيغة، نحصل على:

الميل = (3 – 1) / (4 – 2) = 2 / 2 = 1
2. حساب التغير في الارتفاع (Δy)
يُحسب التغير في الارتفاع عن طريق طرح إحداثي الارتفاع للنقطة الأولى (y1) من إحداثي الارتفاع للنقطة الثانية (y2).
في مثالنا، لدينا:
Δy = y2 – y1 = 3 – 1 = 2
3. حساب التغير في المدى (Δx)
يُحسب التغير في المدى عن طريق طرح إحداثي المدى للنقطة الأولى (x1) من إحداثي المدى للنقطة الثانية (x2).
في مثالنا، لدينا:
Δx = x2 – x1 = 4 – 2 = 2
4. حساب الميل
بمجرد حساب Δy و Δx، يمكننا حساب ميل المستقيم باستخدام الصيغة:


الميل = Δy / Δx

في مثالنا، لدينا:
الميل = 2 / 2 = 1
5. تفسير الميل
يخبرنا ميل المستقيم بشيئين عن الخط:
- اتجاه الخط: إذا كان الميل موجبًا، فإن الخط يميل إلى الأعلى من اليسار إلى اليمين. إذا كان الميل سالبًا، فإن الخط يميل إلى الأسفل من اليسار إلى اليمين.
- انحدار الخط: يشير مقدار الميل إلى مدى انحدار الخط. فكلما زاد الميل، كلما كان الخط أكثر انحدارًا.
6. خطوط خاصة
هناك بعض الخطوط ذات الميل الخاص:
- خط أفقي: الميل = 0
- خط رأسي: الميل غير معرف (لا نهائي)
- خط متطابق: الميل = 1
7. تطبيقات ميل المستقيم
لميل المستقيم تطبيقات عديدة في الرياضيات والعلوم، بما في ذلك:
- إيجاد معادلة الخط
- تحديد نوع الخط (خطي، مكافئ، إلخ)
- حساب الزوايا بين الخطوط
الخلاصة
ميل المستقيم هو رقم يصف مدى انحدار الخط. يتم حسابه باستخدام الصيغة ميل = Δy / Δx، حيث Δy هو التغير في الارتفاع وΔx هو التغير في المدى بين نقطتين على الخط. يخبرنا ميل المستقيم عن اتجاه وانحدار الخط ولها تطبيقات عديدة في الرياضيات والعلوم.