( أي العبارات التالية تصف العلاقة الممثلة في الشكل المقابل )
العلاقة الممثلة في الشكل المقابل
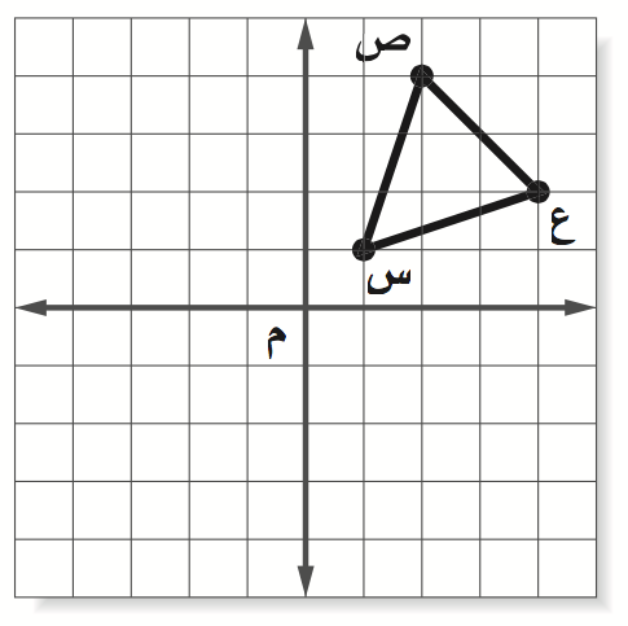
تُمثل العلاقة الموضحة في الشكل المقابل علاقة تناسب طردي. في العلاقة ذات التناسب الطردي، تتغير المتغيران المتعلقان بنفس النسبة. بعبارة أخرى، عندما يزداد أحد المتغيرين، يزداد المتغير الآخر بنفس المقدار. يُشار إلى العلاقة ذات التناسب الطردي غالبًا بالرمز “∝”.
خصائص العلاقة ذات التناسب الطردي
1. تغير ثابت: تتغير المتغيران المتناسبان بنفس النسبة. تُعرف هذه النسبة باسم معامل التناسب.
2. المرور عبر الأصل: تمر العلاقة ذات التناسب الطردي دائمًا عبر نقطة الأصل (0,0). وهذا يعني أنه عندما يكون أحد المتغيرين صفرًا، يكون المتغير الآخر أيضًا صفرًا.
3. خط مستقيم: يُمثل العلاقة ذات التناسب الطردي خط مستقيم على مخطط بياني. يكون منحدر الخط مساويًا لمعامل التناسب.

حساب معامل التناسب
معامل التناسب هو ثابت يحدد نسبة تغير المتغيرين المتناسبين. يمكن حسابه باستخدام الصيغة التالية:

“`
معامل التناسب = تغيير المتغير 1 / تغيير المتغير 2
“`

حيث:
تغيير المتغير 1 هو مقدار تغير المتغير الأول.
تغيير المتغير 2 هو مقدار تغير المتغير الثاني.
أمثلة على العلاقات ذات التناسب الطردي
هناك العديد من الأمثلة على العلاقات ذات التناسب الطردي في العالم الحقيقي، بما في ذلك:
1. مسافة ووقت: المسافة التي يقطعها جسم يتحرك بسرعة ثابتة تتناسب طرديًا مع الوقت الذي يقضيه في السفر.
2. القوة والمساحة: القوة اللازمة لتحريك جسم عبر مسافة معينة تتناسب طرديًا مع المسافة.
3. الحجم والسعر: حجم عنصر معين يتناسب طرديًا مع سعره.

العلاقة العكسية
تُعرف العلاقة التي يتغير فيها متغيران بنسب عكسية باسم العلاقة العكسية. في العلاقة العكسية، عندما يزداد أحد المتغيرين، ينقص المتغير الآخر. يُشار إلى العلاقة العكسية غالبًا بالرمز “∝”.
خصائص العلاقة العكسية
1. تغير عكسي: يتغير المتغيران المتناسبان بنسب عكسية.
2. عدم المرور عبر الأصل: لا تمر العلاقة العكسية عادةً عبر نقطة الأصل.
3. خط منحني: يُمثل العلاقة العكسية خط منحني على مخطط بياني. يكون حاصل ضرب المتغيرين المتناسبين ثابتًا.
حساب معامل التناسب في العلاقة العكسية
معامل التناسب في العلاقة العكسية هو أيضًا ثابت يحدد نسبة تغير المتغيرين المتناسبين. يمكن حسابه باستخدام الصيغة التالية:

“`
معامل التناسب = حاصل ضرب المتغير 1 × المتغير 2
“`
حيث:
المتغير 1 هو أحد المتغيرين المتناسبين.
المتغير 2 هو المتغير المتناسب الآخر.
أمثلة على العلاقات العكسية
هناك العديد من الأمثلة على العلاقات العكسية في العالم الحقيقي، بما في ذلك:
1. السرعة والوقت: الوقت المستغرق للسفر إلى وجهة معينة يتناسب عكسيًا مع السرعة التي يسافر بها المرء.
2. القوة والمسافة: القوة اللازمة لتحريك جسم إلى مسافة معينة تتناسب عكسيًا مع المسافة.
3. الحجم والسعر: سعر عنصر معين يتناسب عكسيًا مع حجمه.
الخلاصة
العلاقات ذات التناسب الطردي والعكسية شائعة في العالم الحقيقي. من المهم فهم خصائص كل نوع من العلاقات من أجل حل المشكلات وتحليل البيانات.