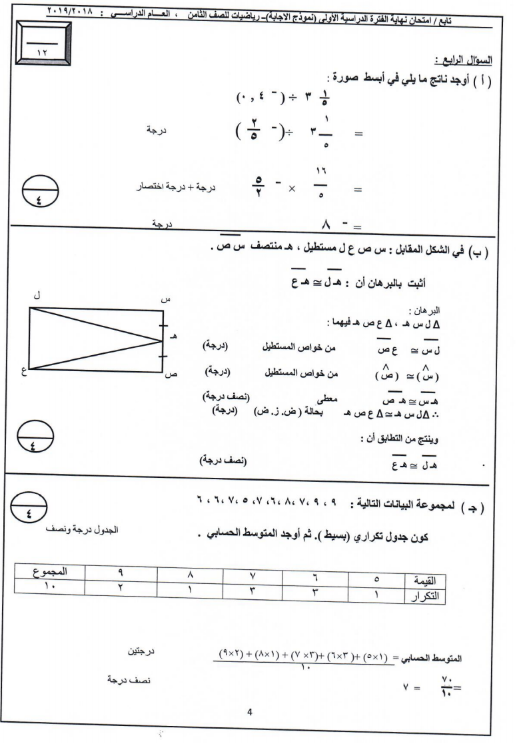
( إذا كان المثلثان ا ب ج و س ص ع متشابهان وكان ا ب = 10 س ص = 2 س ع = 6 فان ا ج = )
المثلثات المتشابهة

مقدمة
المثلثات المتشابهة هي مثلثات لها نفس الشكل ولكنها تختلف في الحجم. هذا يعني أن زوايا المثلثات المتشابهة متساوية، ولكن يمكن أن تختلف أطوال أضلاعها.
خصائص المثلثات المتشابهة
يوجد العديد من الخصائص للمثلثات المتشابهة. فيما يلي بعض من أهم الخصائص:
- زوايا المثلثات المتشابهة متساوية.
- نسب أضلاع المثلثات المتشابهة متساوية.
- نسب مساحات المثلثات المتشابهة متساوية.
استخدامات المثلثات المتشابهة

تُستخدم المثلثات المتشابهة في مجموعة متنوعة من التطبيقات، ومنها:

- حساب المساحات والارتفاعات
- رسم الخرائط والتصميم
- هندسة الإنشاء
إيجاد طول الضلع المجهول في مثلث متشابه
في بعض الأحيان، قد نعرف معلومات حول مثلثين متشابهين ونحتاج إلى إيجاد طول ضلع مجهول في أحد المثلثين. يمكننا استخدام نسب أضلاع المثلثات المتشابهة للقيام بذلك.

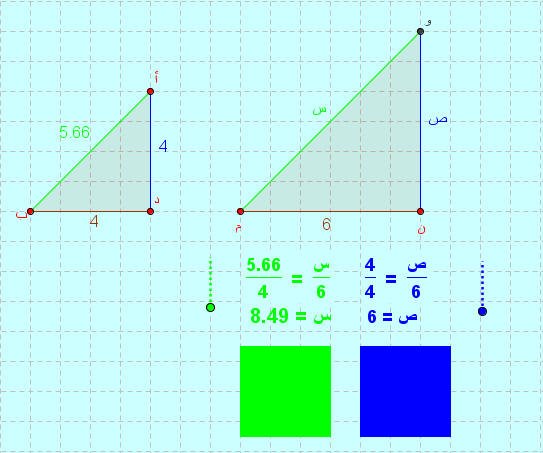
على سبيل المثال، إذا كان لدينا مثلثان متشابهان وكان طول أحد أضلاع المثلث الأول 10سم وطول الضلع المقابل في المثلث الثاني 15سم، فإن نسبة أضلاع المثلثين هي 2:3. هذا يعني أن طول أي ضلع في المثلث الأول يساوي 2/3 طول الضلع المقابل في المثلث الثاني.
إيجاد المساحة المجهولة في مثلث متشابه
يمكننا أيضًا استخدام نسب أضلاع المثلثات المتشابهة لإيجاد المساحة المجهولة في أحد المثلثين. ونفعل ذلك بإيجاد نسبة مساحتي المثلثين ثم استخدامها لإيجاد المساحة المجهولة.
على سبيل المثال، إذا كان لدينا مثلثان متشابهان وكانت مساحة أحد المثلثين 10سم2 ومساحة المثلث الآخر 15سم2، فإن نسبة مساحتي المثلثين هي 2:3. هذا يعني أن مساحة أي مثلث تساوي 2/3 مساحة المثلث الآخر.

الخطوات لحل المسائل المتعلقة بالمثلثات المتشابهة
لحل المسائل المتعلقة بالمثلثات المتشابهة، يمكننا اتباع الخطوات التالية:
- تحديد أن المثلثين متشابهين.
- إيجاد النسب بين أضلاع المثلثين.
- استخدام النسب لحساب المعلومات المطلوبة.
خاتمة
المثلثات المتشابهة هي أداة قوية لحل مجموعة متنوعة من المسائل الهندسية. من خلال فهم خصائص المثلثات المتشابهة، يمكننا إيجاد المعلومات المفقودة وحساب المساحات والارتفاعات وغير ذلك الكثير.